全ての選出と交換に渡る全ての敵の組み合わせを計算 その4 貪欲法
前回の記事で書いた貪欲法の詳細について書きます。
現在位置から先のアイテムaを規制しているゲートの番号の最小値のことをaのcaughtと呼ぶことにします。
ただしそのようなゲートがない場合はN-1を表すことにします(ゲートの番号の最大値がN-2なので)。また現在位置がゲートであるときは、そこから先のゲートとは自身を含むものとします。
次のようなルールに従った選び方を貪欲な選び方と呼ぶことにします。
- shop 0では予定表で決まっている以外の選択は、残された選択肢のうちcaughtの大きなものから順に選ぶことにより決定する
- shop i (i ≧ 1)では:
- 予定表によりここで交換することができない場合はもちろん交換はしない
- 手持ちでここで手放すことが可能であるようなうちcaughtが最小のものをとりaとする
- 予定表により交換することが決まっているなら、aを手放し決まっている交換先をもらう
- 交換することが決まっていないなら、交換先でcaughtが最大のものをbとする。そしてaのcaughtがbのcaught以上なら交換せず、そうでなければaを手放しbを手に入れる
このとき次を示すことが目標となります。
gate iまでの任意の選び方rと貪欲な選び方gに対して次が成立する(i ∈ 0..N-2):
gがgate iで脱落するならrもgate iで脱落する
ただし「gate iまでの選び方」というのは予定表を守っていて、gate iよりも左のゲートをすべて合格しているものに限ります。
ここで必要な補題を示します。
長さLの非負整数の列r, gがある。またs1, s2, t1, t2 ∈ 0...Lがある。
t1, t2はt1 <= t2を満たす。s2はgのうち値が正である最小のインデックスである。またr[s1]は正とする。r'はrと等しいか、rのs1番目を1減らしてt1番目を1増やした列であるかのどちらかであるとする。
s2 < t2のとき、g'はgのs2番目を1減らしてt2番目を1増やした列であり、そうでないときはg'はgそのままの列であるとする。
rとgでは同じ長さの始切片それぞれの要素の総和は常にgの方が小さいか等しいとする。
このとき、r'とg'では同じ長さの始切片それぞれの要素の総和は常にg'の方が小さいか等しい。
証明
l ∈ 0...Lを任意にとる。
列rの長さlの始切片の要素の総和をσ(r)と書くことにする。
σ(g') <= σ(g)であることはかんたんに分かる。
r' = rの場合はσ(g') <= σ(g) <= σ(r) = σ(r')となって成立する。よって、以下r'はrのs2番目を1減らしてt1番目を1増やした列である場合を考える。
g' != g すなわち s2 < t2の場合
rのs1番目を1減らした列をr*, gのs2番目を1減らした列をg*とおく。t1 <= t2から、σ(g*) <= σ(r*)を示せばσ(g') <= σ(r')もわかる。
s2 <= s1のときはかんたんにσ(g*) <= σ(r*)がわかる。
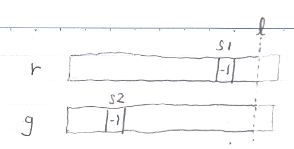
(図でlの位置を動かして考えてみよ)
s1 < s2のとき:
s1番目が始切片の範囲に入っていてs2番目は入っておらず、さらにσ(g) = σ(r)のときが問題となる。(そうでないときは問題なくσ(g*) <= σ(r*)となる)
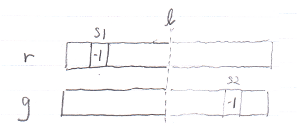
このときs1番目が始切片に入っているのだから、σ(r) ≧ 1となる。よってσ(g) ≧ 1。だからs2番目は始切片の範囲に入っていなければおかしい。よってこの場合はありえない。
g' = g すなわち t2 <= s2の場合
t1 <= s1の場合は明らか。よってs1 < t1とする。
s1番目が始切片の範囲に入っていてt1番目は入っておらず、さらにσ(g) = σ(r)のときが問題となる。

このときs1番目が始切片に入っているのだから、σ(r) ≧ 1となる。よってσ(g) ≧ 1。だからs2番目は始切片の範囲に入っている。しかしl <= t1 <= t2 <= s2であったから矛盾。よってこの場合はありえない。
□
gate iまでの任意の選び方rと貪欲な選び方gに対して次が成立する(i ∈ 0..N-2):
d(r)とd(g)では同じ長さの始切片それぞれの要素の総和は常にd(g)の方が小さいか等しい
ただしd(r)の定義は次の通り:
選び方rの現在位置をgate iとしたときの手持ちのうち、予定表で今持っていることが決められているというわけではないもののリストを考えます。
このリストのうちcaughtがnであるものの個数を第n要素の値(n ∈ 0..N-1)とする長さNの列をd(r)とします。
そしてここから次の目標の命題が従います。
gate iまでの任意の選び方rと貪欲な選び方gに対して次が成立する(i ∈ 0..N-2):
gがgate iで脱落するならrもgate iで脱落する
注
a..bはa以上b以下の整数全体の集合、a...bはa以上b未満の整数全体の集合を表す。
rの始切片とはrの先頭から途中まであるいは末尾までを取り出した列のこと
変数名の由来 r: route, g: greedy, d: distribute