線形合同法数列が最大周期になる条件(ただし法が2のべきの場合)

(追記)もっと簡潔な証明を得ました: 線形合同法数列が最大周期になる条件(ただし法が2のべきの場合) その2 - oupoの日記

はじめに

一部界隈の皆さんはよくご存知の線形合同法数列
　　　 $a_0 = F \bmod 2^{32}$ ( $F$ は初期シード)
　　　 $a_{n+1} = ({\rm 0x41c64e6d} \times a_n + {\rm 0x6073}) \bmod 2^{32}$

は最大周期となることが知られています。
すなわち $a_1$ , $a_2$ , ... と進めていって $a_{2^{32}}$ で初めて $a_0$ と等しくなります。
なぜそんなことがいえるのでしょうか。またどういう条件のときに最大周期になるのでしょうか。

問題

線形合同法数列
　　　 $a_0 = F \bmod M$
　　　 $a_{n+1} = (A a_n + B) \bmod M$
が最大周期となる条件はなにか。

この記事では $M$ が $4$ 以上の $2$ の累乗のときを扱いましょう。つまり $s$ を $2$ 以上の整数として $M = 2^s$ と表せるときです。
( $M = 2$ のときも含めると後に場合分けが必要になるので省きました。ご都合主義です^^;)

具体例

まずは実際に $A$ , $B$ , $M$ , $F$ に具体的な値を入れて数列を眺めてみましょう。

$a_0 = 0$ , $a_{n+1}=(5 a_n + 1) \bmod 8$

$n$ 0 1 2 3 4 5 6 7 8 9

$a_n$ 0 1 6 7 4 5 2 3 0 1

…最大周期となる
$a_0 = 0$ , $a_{n+1}=(5 a_n + 2) \bmod 8$

$n$ 0 1 2 3 4 5 6 7 8 9

$a_n$ 0 2 4 6 0 2 4 6 0 2

…最大周期とならない
$a_0 = 1$ , $a_{n+1}=(5 a_n + 2) \bmod 8$

$n$ 0 1 2 3 4 5 6 7 8 9

$a_n$ 1 7 5 3 1 7 5 3 1 7

…最大周期とならない
$a_0 = 0$ , $a_{n+1}=(4 a_n + 1) \bmod 8$

$n$ 0 1 2 3 4 5 6 7 8 9

$a_n$ 0 1 5 5 5 5 5 5 5 5

…最大周期とならない

$n$	0	1	2	3	4	5	6	7	8	9
$a_n$	0	1	6	7	4	5	2	3	0	1

$n$	0	1	2	3	4	5	6	7	8	9
$a_n$	1	7	5	3	1	7	5	3	1	7

$n$	0	1	2	3	4	5	6	7	8	9
$a_n$	0	1	5	5	5	5	5	5	5	5

$F=0$ としても一般性は失われない

実は $A$ , $B$ , $M$ の $3$ つが決まれば、初期シード $F$ によらず最大周期になるかどうかは決まります。
これを証明すれば、後の議論において $F = 0$ の場合だけ考えればよいことになり楽できます。

それを証明するための準備として周期に関する性質をまとめておきます。

周期に関する性質

具体的なところから、線形合同法数列 $\< a_n\>$ が $a_4$ で初めて $a_0$ の値に戻ってくるものとします。数列の項の具体的な値は今は重要ではないので $a$ , $b$ , $c$ , $d$ としましょう。

ここで重要になってくるのは線形合同法数列がもつ、 $a_i = a_j$ ならば $a_{i+1} = a_{j+1}$ という性質です。

数列の項の変化を図に表すと次のようになりますね。

ここで $a_0$ , $a_1$ , $a_2$ , $a_3$ の値にダブりはあるでしょうか？　ありません。
まず、 $a_1$ , $a_2$ , $a_3$ のいずれかが $a_0$ に等しいとすると「 $a_4$ で初めて $a_0$ の値に戻る」ということに反するのでありえません。
次に $a_1$ , $a_2$ , $a_3$ の中でダブりがあるとするとそこでループができてしまって二度と $a_0$ の値には戻ってきません。
たとえば $a_1 = a_3$ のとき次のようになります。

以上の議論は周期が $4$ 以外のときも成り立ちます。これは直感的理解のための説明です。ちゃんとした証明も難しくはありませんが、この記事では省略します。

上記の説明の通り、線形合同法数列 $a_n$ が $a_M$ で初めて $a_0$ の値に戻ってくるとき、 $a_0$ , $a_1$ , $a_2$ , $\cdots$ , $a_{M-1}$ は互いに異なります。互いに異なるのだからこれらは $M$ 個の値からなります。
ここで数列 $a_n$ の項はすべて $0$ 以上 $M$ 未満である $M$ 個の整数の中からとるのですから、 $a_0$ , $a_1$ , $a_2$ , $\cdots$ , $a_{M-1}$ には $0$ 以上 $M$ 未満の整数が一つずつ現れるといえます。

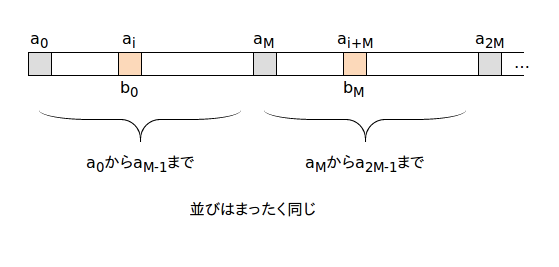
$F=0$ としても一般性は失われないことの証明

任意の $f_1$ , $f_2$ について、 $F = f_1$ で最大周期となるならば $F = f_2$ で最大周期となることを証明すればよいです。

なぜならこれが正しいとすると、

$f_1=0$ , $f_2=f$ をあてはめて、 $F = 0$ で最大周期ならば $F = f$ で最大周期であること
$f_1=f$ , $f_2=0$ をあてはめて、 $F = f$ で最大周期ならば $F = 0$ で最大周期であること

がいえますから、任意の $f$ について、 $F = 0$ で最大周期であることと $F = f$ で最大周期であることが同値になります。

さて、任意の $f_1$ , $f_2$ について、 $F = f_1$ で最大周期となるならば $F = f_2$ で最大周期となることを証明しましょう。
$F=f_1$ のときの数列を $\< a_n\>$ , $F=f_2$ のときの数列を $\< b_n\>$ とします。

$\< a_n\>$ は最大周期となるのだから、「周期に関する性質」より $a_i = f_2 \bmod M$ , $0 \le i < M$ となる整数 $i$ が存在しますね。
$a_i = b_0$ であり、二つの数列の漸化式は同じなのだから任意の $k$ について $a_{i+k} = b_k$ といえます。

えーここでもちゃんとした証明がめんどくさくなったので^^;、図を使った直感的な説明に逃げます。

これを見ると $a_i$ から $a_{i+M-1}$ までにダブりがない、すなわち $b_0$ から $b_{M-1}$ までにダブりがない。また、 $a_i = a_{i+M}$ すなわち $b_0 = b_M$ だと直感的理解ができますね。

よって数列 $\< b_n\>$ は最大周期になります。
したがって、任意の $f_1$ , $f_2$ について、 $F = f_1$ で最大周期となるならば $F = f_2$ で最大周期となるといえます。

$F=0$ としても一般性は失われないことが示されましたので、以降からは $F=0$ の場合だけ考えましょう。

一般項

まず $a_n$ は必ず $0$ 以上 $M$ 未満の整数となりますから $a_n = (a_n \bmod M)$ が常に成り立ちます。
ここで数列 $a_n$ の一般項を求めてみましょう。

実際に最初の数項を観察してみると

いずれも $M$ を法として
　　　 $a_0 \equiv 0$
　　　 $a_1 \equiv A \times a_0 + B \equiv B$
　　　 $a_2 \equiv A \times a_1 + B \equiv A \times B + B = (A + 1) B$
　　　 $a_3 \equiv A \times a_2 + B \equiv A \times (A + 1) B + B = (A^2 + A + 1) B$

より
　　　 $a_n \equiv (1 + A + \cdots + A^{n-1}) B \pmod{M}$
と予想できます。この予想が正しければ、

　　　 $a_n \bmod M = ( (1 + A + \cdots + A^{n-1}) B) \bmod M$
　　　よって $a_n = ( (1 + A + \cdots + A^{n-1}) B) \bmod M$ （ $a_n = a_n \bmod M$ より）

となります。
つまり一般項は $a_n = ( (1 + A + \cdots + A^{n-1}) B) \bmod M$ と予想できますね。
この予想は数学的帰納法で簡単に証明できます。（省略）

補足
ここではさらっと次の定理を使いました。
$a \equiv b \pmod{m}$ ならば $a + c \equiv b + c \pmod{m}$ 、 $ac \equiv bc \pmod{m}$
この定理は $m=10$ のときで考えてみるととっても当たり前です。
足し算や掛け算した結果の一の位は、足す数や掛ける数の一の位だけで決まりますからね。

$B$ が偶数のとき？

まずは簡単なところから条件を絞っていきます。 $B$ が偶数であるとするとどうなるでしょう。
最初の具体例の一つにもう一度ご登場願いましょう。

$a_0 = 0$ , $a_{n+1}=(5 a_n + 2) \bmod 8$

$n$	0	1	2	3	4	5	6	7	8	9
$a_n$	0	2	4	6	0	2	4	6	0	2

$M$ も偶数なので $a_n$ は常に偶数となってしまいます。 $(a_n$ が(偶数)を $M$ で割った余りであり $a_n =$ (偶数) $- M \times$ (商)と表せるから)
しかし、最大周期のとき $a_0$ , $a_1$ , $\cdots$ , $a_{M-1}$ は $0$ から $M-1$ までのすべての整数をとるはずだったので、 $B$ が偶数だとこれに反しますね。
よって、 $B$ が偶数のときは最大周期になりません。

$A$ が偶数のとき？

では、 $A$ が偶数のときはどうでしょう。

$A$ が偶数かつ最大周期だと仮定します。
ここで周期に関する性質より $a_i = M/2$ , $0 \le i < M$ を満たす整数 $i$ があります。 $M/2\ne 0$ だから $i=0$ はないですね。
$A$ は $2$ の倍数だから $A a_i$ は $M$ の倍数となります。
$M$ の倍数の違いは $M$ で割った余りには影響しませんから、
　　　 $\begin{eqnarray}\\ a_{i+1} &=& (A a_i + B) \bmod M\\ &=& B \bmod M\\ \end{eqnarray}$
よって $a_{i+1} = a_1$ です。 $a_1$ , $a_2$ , ..., $a_M$ は互いに異なりますから矛盾しました。（これは $a_0$ , $a_1$ , ..., $a_{M-1}$ が互いに異なることと $a_M = a_0$ からすぐ分かります）

補足
二進数で考えてみるとAが偶数だったら現在の項の最上位ビットが次の項にまったく影響しません。すると最上位ビットが異なりほかのビットは一致する2つのシード値において、それぞれの次のシード値が一致することになります。このとき直感的に明らかに最大周期にはなりませんね。このことをちゃんと証明したのが上の内容です。

さらに補足
$a_0 = 0$ , $a_{n+1}=(4 a_n + 1) \bmod 8$

$n$ 0 1 2 3 4 5 6 7 8 9

$a_n$ 0 1 5 5 5 5 5 5 5 5

この具体例のようにAが偶数だった場合は必ず一定値に収束してしまいます。擬似乱数としてはまったく使い物になりませんね。
余談ですが、あるゲームのあるデータの難読化用XORマスクとしてAが偶数である線形合同法数列が使われていました^^;この例では別に擬似乱数としてぶっ壊れていても全然差し支えはないですが、もしゲーム中のランダム要素でこうなっていたら大変なことになりますね

$n$	0	1	2	3	4	5	6	7	8	9
$a_n$	0	1	5	5	5	5	5	5	5	5

さて、 $A$ か $B$ のどちらか少なくとも一方が偶数のときは最大周期にならないことは分かったので、以降では $A$ 、 $B$ ともに奇数である場合を調べましょう。

$a_n = 0$ という条件

最大周期となるというのは、 $a_M$ で初めて $a_0$ の値に戻ってくるということでした。
つまり $a_M = 0$ かつ $1 \le n < M$ であるすべての $n$ について $a_n \ne 0$ であるということです。

ということは $n$ に対して $a_n$ が $0$ になるかどうかが重要になります。 $a_n = 0$ であるかどうかという条件を変形していきましょう。

　　　 $a_n = 0$
　　　 $\Leftrightarrow ( (1 + A + \cdots + A^{n-1}) B) \bmod M = 0$
　　　 $\Leftrightarrow (1 + A + \cdots + A^{n-1}) B$ が $M$ の倍数
　　　 $\Leftrightarrow (1 + A + \cdots + A^{n-1}) B$ が $2^s$ の倍数
　　　 $\Leftrightarrow (1 + A + \cdots + A^{n-1})$ が $2^s$ の倍数 ( $B$ は奇数より)

よって $(1 + A + \cdots + A^{n-1})$ が $2$ の何乗で割れるかに注目しましょう。

正整数 $x$ が $2^k$ で割り切れるような最大の $k$ を $v_2(x)$ で表すことにします。

$D_A(n) = (1 + A + \cdots + A^{n-1})$ とおきます。

すると
　　　 $a_n = 0 \Leftrightarrow v_2(D_A(n)) \ge s$
となります。（ただし $n>0$ とする。 $n=0$ のとき $D_A(n)=0$ で $v_2(0)$ は求まらないから）

$v_2(D_A(n))$ を観察する

ここで $v_2(D_A(n))$ が実際どうなるのか具体的に見てみましょう。

$A=3$ のとき

$n$	$D_A(n)$	$v_2(D_A(n))$
1	$1=1$	0
2	$1+3=4$	2
3	$1+3+3^2=13$	0
4	$1+3+3^2+3^3=40$	3
5	$1+3+3^2+3^3+3^4=121$	0
6	$1+3+3^2+3^3+3^4+3^5=364$	2
7	$1+3+3^2+3^3+3^4+3^5+3^6=1093$	0
8	$1+3+3^2+3^3+3^4+3^5+3^6+3^7=3280$	4
9	$1+3+3^2+3^3+3^4+3^5+3^6+3^7+3^8=9841$	0
10	$1+3+3^2+3^3+3^4+3^5+3^6+3^7+3^8+3^9=29524$	2

$v_2(D_A(n))$ になにか規則性はないか睨んでみると、 $v_2(D_A(n))$ は $v_2(n)$ と関係がありそうだとわかります。

$n$	$v_2(n)$	$v_2(D_A(n))$
1	0	0
2	1	2
3	0	0
4	2	3
5	0	0
6	1	2
7	0	0
8	3	4
9	0	0
10	1	2

$n$ が偶数のときは $v_2(D_A(n)) = v_2(n) + 1$ 、 $n$ が奇数のときは $v_2(D_A(n)) = 0$ となっていそうです。

$n$ が奇数のとき $0$ になるのは当たり前ですね。奇数を奇数個集めた和は奇数になりますから。
よって $n$ が偶数の場合のみを追って $A=3$ 以外も試してみます。さすがに $A$ が大きくなると計算が大変になるのでコンピュータに計算させました^^;
$v_2(D_A(n))$ の表

$A$ ＼ $n$	2	4	6	8	10
1	1	2	1	3	1
3	2	3	2	4	2
5	1	2	1	3	1
7	3	4	3	5	3
9	1	2	1	3	1
11	2	3	2	4	2
13	1	2	1	3	1
15	4	5	4	6	4
17	1	2	1	3	1
19	2	3	2	4	2
21	1	2	1	3	1
23	3	4	3	5	3
25	1	2	1	3	1
27	2	3	2	4	2
29	1	2	1	3	1
31	5	6	5	7	5

$\< v_2(2), v_2(4), v_2(6), v_2(8), v_2(10)\> = \< 1,2,1,3,1\>$ ですから、何かに $v_2(n)$ を足した結果が $v_2(D_A(n))$ になっていそうですね。
$v_2(n)$ を引いた結果を表にしてみると

$v_2(D_A(n)) - v_2(n)$ の表

$A$ ＼ $n$	2	4	6	8	10
1	0	0	0	0	0
3	1	1	1	1	1
5	0	0	0	0	0
7	2	2	2	2	2
9	0	0	0	0	0
11	1	1	1	1	1
13	0	0	0	0	0
15	3	3	3	3	3
17	0	0	0	0	0
19	1	1	1	1	1
21	0	0	0	0	0
23	2	2	2	2	2
25	0	0	0	0	0
27	1	1	1	1	1
29	0	0	0	0	0
31	4	4	4	4	4

$15$ のとき $3$ 、 $31$ のとき $4$ …、 $15$ は $2^4-1$ で $31$ は $2^5-1$ だから…と考えるとこの数値は $v_2(A+1)-1$ に等しいと気づきます。つまり $v_2(D_A(n)) - v_2(n) = v_2(A+1) - 1$ です。

まとめますと、

$n$ が奇数のとき	$v_2(D_A(n)) = 0$
$n$ が偶数のとき	$v_2(D_A(n)) = v_2(n) + v_2(A+1) - 1$

ということです。

しかしこれは $A$ や $n$ が小さいときの結果からの予想に過ぎないので、実際にすべての $A$ や $n$ で成り立つことは証明しないといけません。

偶数 $n>0$ について $v_2(D_A(n)) = v_2(n) + v_2(A+1) - 1$ の証明

さあ、ここが一番やっかいそうなところです。

関数 $v_2(x)$ は $v_2(x \times y) = v_2(x) + v_2(y)$ という対数関数のような性質を持ちます。
$i = v_2(x)$ , $j = v_2(y)$ とすると $m$ , $n$ を奇数として $x = 2^i m$ , $y = 2^j n$ と表せますから、 $x \times y = (2^i m) \times (2^j n) = 2^{i+j} (mn)$ で $mn$ は奇数より $v_2(x \times y) = i + j$ となるからです。

変形

$n = 2k$ とおいて、証明すべき命題を変形しましょう。
　　　 $v_2(D_A(2k)) = v_2(2k) + v_2(A+1) - 1$
$v_2(2k) = v_2(2) + v_2(k)$ を使って
　　　 $\Leftrightarrow v_2(D_A(2k)) = (1 + v_2(k)) + v_2(A+1) - 1$
等式の右辺を整理して
　　　 $\Leftrightarrow v_2(D_A(2k)) = v_2(k) + v_2(A+1)$
両辺に $v_2(A-1)$ を足して
　　　 $\Leftrightarrow v_2(D_A(2k)) + v_2(A-1) = v_2(k) + v_2(A+1) + v_2(A-1)$
$v_2(x) + v_2(y) = v_2(x \times y)$ を使って
　　　 $\Leftrightarrow v_2(D_A(2k) \times (A-1)) = v_2(k) + v_2( (A+1) \times (A-1))$
ここで
　　　 $\begin{eqnarray}\\ D_A(2k) \times (A-1) &=& (1 + A + \cdots + A^{2k-1}) \times (A - 1)\\ &=& A^{2k} - 1\\ \end{eqnarray}$
だから (等比数列の和の公式の分母を払った形ですね)
　　　 $\Leftrightarrow v_2(A^{2k} - 1) = v_2(k) + v_2(A^2-1)$
さらに $c=A^2$ とおくと
　　　 $\Leftrightarrow v_2(c^{k} - 1) = v_2(k) + v_2(c-1)$
となります。

おっと、 $A=1$ のときは $v_2(A-1)=v_2(0)$ は求まりませんから、 $A=1$ のときは別に議論をちゃちゃっと済ませちゃいましょう。
$A=1$ のとき $D_A(n)=n$ だから $v_2(D_A(n)) = v_2(n)$ 。また、 $v_2(A+1) - 1 = v_2(2) - 1 = 0$ だから $v_2(D_A(n)) = v_2(n) + v_2(A+1) - 1$ が成り立ちます。

具体的な $k$ の値で考えてみる

具体的な $k$ の値として $k=10$ で考えてみます。

$c^{10} - 1$ を因数分解します。
　　　 $\begin{eqnarray}\\ c^{10} - 1 &=& (c^5 - 1) \times (c^5 + 1)\\ &=& (c - 1) \times (1 + c + c^2 + c^3 + c^4) \times (c^5 + 1)\\ \end{eqnarray}$
より
　　　 $v_2(c^{10} - 1) = v_2(c - 1) + v_2(1 + c + c^2 + c^3 + c^4) + v_2(c^5 + 1)$
です。

すると、証明すべき等式
　　　 $v_2(c^{10} - 1) = v_2(c - 1) + v_2(10)$
をいうためには、二つの式を見比べると
　　　 $v_2(1 + c + c^2 + c^3 + c^4) + v_2(c^5 + 1) = v_2(10)$
つまり、 $v_2(10) = 1$ より
　　　 $v_2(1 + c + c^2 + c^3 + c^4) + v_2(c^5 + 1) = 1$
がいえればいいですね。

$v_2(1 + c + c^2 + c^3 + c^4)$ はすぐわかります。 $A$ は奇数より $c = A^2$ は奇数だから奇数を奇数個集めた和は奇数より、これは $0$ になります。
するとあとは $v_2(c^5 + 1) = 1$ がいえればいいはずです。 $v_2$ の値が $1$ というのは $2$ で割り切れ $4$ で割り切れないということですから $4$ で割った余りを考えましょう。

$c=A^2$ であり、 $A$ は奇数です。
奇数の $2$ 乗は必ず $4$ で割った余りが $1$ になります。また $4$ で割った余りが $1$ である数同士の積は再び $4$ で割った余りが $1$ になります。（これは奇数を $2n+1$ とおいたり、 $4$ で割った余りが $1$ である二数を $4n+1$ と $4m+1$ とおいたりして実際に計算してみれば明らかです）
よって $c$ の累乗は常に $4$ で割った余りが $1$ になります。

よって $c^5 \bmod 4 = 1$ より $(c^5 + 1) \bmod 4 = 2$ です。よって $v_2(c^5 + 1) = 1$ がいえます。
これで $k=10$ のとき証明すべき $v_2(c^k - 1) = v_2(c - 1) + v_2(k)$ がいえました。

また、同じようにしてk=5のときの
　　　 $\begin{eqnarray}\\ v_2(c^5 - 1) &=& v_2(c - 1) + v_2(1 + c + c^2 + c^3 + c^4)\\ &=& v_2(c - 1) + 1\\ &=& v_2(c - 1) + v_2(5)\\ \end{eqnarray}$
もいえます。

そうなると $k=10$ の場合は $k=5$ を先に証明しておいてから、その結果を使えばいいですね。

　　　 $v_2(c^{10} - 1) = v_2(c^5 - 1) + v_2(c^5 + 1)$
より $k=5$ の結果 $v_2(c^5 - 1) = v_2(c - 1) + v_2(5)$ を使って
　　　 $\begin{eqnarray}\\ v_2(c^{10} - 1) &=& v_2(c - 1) + v_2(5) + v_2(c^5 + 1)\\ &=& v_2(c - 1) + v_2(5) + 1\\ &=& v_2(c - 1) + v_2(10)\\ \end{eqnarray}$

同様に $k=20$ の場合は、 $k=10$ の結果を使って

　　　 $\begin{eqnarray}\\ v_2(c^{20} - 1) &=& v_2(c^{10} - 1) + v_2(c^{10} + 1)\\ &=& v_2(c - 1) + v_2(10) + v_2(c^{10} + 1)\\ &=& v_2(c - 1) + v_2(10) + 1\\ &=& v_2(c - 1) + v_2(20)\\ \end{eqnarray}$

$k=40$ の場合は、 $k=20$ の結果を使って
　　　 $\begin{eqnarray}\\ v_2(c^{40} - 1) &=& v_2(c^{20} - 1) + v_2(c^{20} + 1)\\ &=& v_2(c - 1) + v_2(20) + v_2(c^{20} + 1)\\ &=& v_2(c - 1) + v_2(20) + 1\\ &=& v_2(c - 1) + v_2(40)\\ \end{eqnarray}$

…と $k$ が $5$ に $2$ の累乗数をかけた数のときは帰納的に示せれそうです。
それどころか、同じ方法で $5$ でなくても $k$ が奇数 $m$ に $2$ の累乗数をかけた数のとき、つまり任意の正整数 $k$ についていえるんじゃないでしょうか。

やってみましょう。

証明

$i=v_2 k$ として、 $k = 2^i m$ ( $m$ は奇数)と表します。
$v_2(c^{2^i m} - 1) = v_2(c - 1) + i$ が成り立つことを $i$ に関する帰納法で示します。

$i = 0$ のとき

　　　 $\begin{eqnarray}\\ v_2(c^{2^i m} - 1) &=& v_2(c^m - 1)\\ &=& v_2(c - 1) + v_2(1 + c + \cdots c^{m-1})\\ \end{eqnarray}$
であり、 $1 + c + \cdots c^{m-1}$ は奇数を奇数個集めた和だから $v_2(1 + c + \cdots c^{m-1}) = 0$ となり、
　　　 $v_2(c^{2^i m} - 1) = v_c(c - 1)$
より成り立ちます。

$i = l$ のとき成り立つと仮定します。
$v_2(c^{2^l m} - 1) = v_2(c - 1) + l$ です。
$c$ の累乗は $4$ で割った余りが $1$ だから、 $v_2(c^{2^l m} + 1) = 1$

　　　 $\begin{eqnarray}\\ v_2(c^{2^{l+1} m} - 1) &=& v_2(c^{2^l m} - 1) + v_2(c^{2^l m} + 1)\\ &=& v_2(c - 1) + l + 1\\ \end{eqnarray}$
より $i = l + 1$ でも成り立ちます。

よって数学的帰納法により任意の整数 $i \ge 0$ について $v_2(c^{2^i m} - 1) = v_2(c - 1) + i$ が成り立ちます。

これで任意の正整数 $k$ について $v_2(c^{k} - 1) = v_2(k) + v_2(c-1)$ が示されました。
したがって最初の同値変形から任意の偶数 $n>0$ について $v_2(D_A(n)) = v_2(n) + v_2(A+1) - 1$ が成り立ちます。

ラストスパート！

ここでわかっていることを整理しておきましょう。

最大周期となるというのは $a_M = 0$ かつ $1 \le n < M$ であるすべての $n$ で $a_n \ne 0$ であること
任意の $n \ge 1$ について $a_n = 0$ となる条件は $v_2(D_A(n)) \ge s$
$n$ が奇数なら $v_2(D_A(n)) = 0$
$n$ が偶数なら $v_2(D_A(n)) = v_2(n) + v_2(A+1) - 1$ ( $n \ne 0$ )

$v_2(A+1)$ に具体的な値を入れて考えてみます。 $A$ は奇数より $A+1$ は偶数だから $v_2(A+1) = 0$ はないですね。よってまずは、 $1$ のときです。

$v_2(A+1) = 1$ のとき

このとき、 $n$ が偶数なら $v_2(D_A(n)) = v_2(n) + v_2(A+1) - 1 = v_2(n)$ で $n$ が奇数なら $v_2(D_A(n)) = 0$ となります。これは $v_2(D_A(n)) = v_2(n)$ と一つにまとめられますね。

$1 \le n < M (= 2^s)$ であるすべての $n$ について $n$ は $2^s$ で割り切れないので、 $v_2(n) < s$ よって $v_2(D_A(n)) < s$ より $a_n \ne 0$ です。
$n = M$ のとき $v_2(n) = s$ より $a_n = 0$ です。

よって数列は最大周期となります！

$v_2(A+1) = 2$ のとき

このときは $n$ が偶数なら $v_2(D_A(n)) = v_2(n) + 1$ で $n$ が奇数なら $v_2(D_A(n)) = 0$ です。
$1 \le n < 2^s$ の中に $v_2(n) + 1$ が $s$ 以上となるような偶数 $n$ はあるか…。
ありますね、 $n = 2^{s-1}$ です。
よって、 $v_2(D_A(2^{s-1})) = s$ となりますから、 $a_{2^{s-1}} = 0$ です。はい、最大周期になりません！

さあ次は $v_2(A+1) = 3$ のとき…とその必要はありません。 $2$ のときと同様に $3$ 以上のときも $v_2(D_A(2^{s-1})) \ge s$ となりますから。最大周期になりません。

よって $v_2(A+1) = 1$ ならば最大周期となって、そうでないときは最大周期となりません。
$v_2(A+1) = 1$ は言い換えると $(A+1) \bmod 4 = 2$ 、すなわち $A \bmod 4 = 1$ です。

はい、これでひと仕事おしまい。

補足
ここで $s \ge 2$ としておいた布石がきいてます^^; $s=1$ だと $2^{s-1}$ は偶数になりませんからね。

結論

線形合同法数列
　　　 $a_0 = F \bmod M$
　　　 $a_{n+1} = (A a_n + B) \bmod M$
ただし $M = 2^s$ ( $s$ は $2$ 以上の整数)

が最大周期となる条件は
　　　「 $B$ が奇数かつ $A \bmod 4=1$ 」
です。
（ $A$ が奇数であることは $A \bmod 4=1$ からいえるので省いていいのです）

おわりに

線形合同法Ｘn+1=（Ｘn＊A）＋B ｍｏｄ Mが最大周期を持つときの条件を証... - Yahoo!知恵袋

この記事のほとんどは上記のページに負っています。感謝です。

数学をちゃんと学び始める前の頃の自分でも理解できることを目標として平坦になるよう心がけましたがどうなったでしょうね^^;
最大周期となる条件だけでひいひい言っていますが、線形合同法にはまだまだ面白い宝物が隠されているんじゃないかと思っています。

$A$ ＼ $n$	2	4	6	8	10
1	1	2	1	3	1
3	2	3	2	4	2
5	1	2	1	3	1
7	3	4	3	5	3
9	1	2	1	3	1
11	2	3	2	4	2
13	1	2	1	3	1
15	4	5	4	6	4
17	1	2	1	3	1
19	2	3	2	4	2
21	1	2	1	3	1
23	3	4	3	5	3
25	1	2	1	3	1
27	2	3	2	4	2
29	1	2	1	3	1
31	5	6	5	7	5

$A$ ＼ $n$	2	4	6	8	10
1	0	0	0	0	0
3	1	1	1	1	1
5	0	0	0	0	0
7	2	2	2	2	2
9	0	0	0	0	0
11	1	1	1	1	1
13	0	0	0	0	0
15	3	3	3	3	3
17	0	0	0	0	0
19	1	1	1	1	1
21	0	0	0	0	0
23	2	2	2	2	2
25	0	0	0	0	0
27	1	1	1	1	1
29	0	0	0	0	0
31	4	4	4	4	4

$A$ ＼ $n$	2	4	6	8	10
1	1	2	1	3	1
3	2	3	2	4	2
5	1	2	1	3	1
7	3	4	3	5	3
9	1	2	1	3	1
11	2	3	2	4	2
13	1	2	1	3	1
15	4	5	4	6	4
17	1	2	1	3	1
19	2	3	2	4	2
21	1	2	1	3	1
23	3	4	3	5	3
25	1	2	1	3	1
27	2	3	2	4	2
29	1	2	1	3	1
31	5	6	5	7	5

$A$ ＼ $n$	2	4	6	8	10
1	0	0	0	0	0
3	1	1	1	1	1
5	0	0	0	0	0
7	2	2	2	2	2
9	0	0	0	0	0
11	1	1	1	1	1
13	0	0	0	0	0
15	3	3	3	3	3
17	0	0	0	0	0
19	1	1	1	1	1
21	0	0	0	0	0
23	2	2	2	2	2
25	0	0	0	0	0
27	1	1	1	1	1
29	0	0	0	0	0
31	4	4	4	4	4

はじめに

問題

具体例

としても一般性は失われない