AtCoder Regular Contest #013 D問題 切り分けできるかな?
AtCoderの過去問としてARC#013をやってみましたが、さんざんな結果でした。
C問題は以下に解説がありますので、ここではD問題の解説をします。
D問題の問題文:
参考にしたソースコード: (蟻本の著者の一人でもあるiwiwiさんによる提出です)
これは二部マッチングに帰着させて解く問題だったようですね。
最大マッチングに帰着できること
最大マッチングに帰着できることは簡単にわかります。
まず必要になる分銅を表す頂点を用意します。つまり作れる分銅の重さがn通りあれば頂点は2n個あります。
次に1つの鉄塊を切断して作ることにする2つの分銅の頂点同士を結びます。このとき必要になる鉄塊の個数は(頂点数) - (辺数)となります。
さて、これを最小化する鉄塊の切断の仕方(すなわち辺の結び方)を作るには、1つの鉄塊を切断して得られる2つの重さであるような異なる2頂点の対をすべて辺で結んでおき最大マッチングを求めればよいのです。
左右対称なグラフの最大マッチングに関する命題
さて二部マッチングに帰着できることは次の命題を証明すればよいです。
G=(V,E)を無向単純グラフとする。
頂点集合Vは同じ要素数の2つの族L = {l_1, …, l_n}, R = {r_1, …, r_n}に分割できるとする。
また、各i, j = 1, 2, …, nについて
l_iとr_jが接続している <=> r_iとl_jが接続している
l_iとl_jが接続している <=> r_iとr_jが接続している
が成り立つとする。このとき同じ族の頂点同士を結ぶ辺を使わない、グラフGの最大マッチングがある。
ラフな言い方をすれば「頂点を左右2つの族に分割できて、グラフが左右対称になるなら、同じ族の頂点同士を結ぶ辺を使わない最大マッチングがある」といったところです。 (最初はもっとこの問題に特殊化した命題を証明したのですが、後日この形に一般化できることを気づきました)
今回の問題のグラフはこの命題の前提を満たします。なぜなら頂点は同じ重さのペアに分けられますが、同じペアの2つの頂点を別々の族に入れればいいからです。
そして、「同じ族の頂点同士を結ぶ辺を使わない最大マッチングがある」ということから、同じ族の頂点同士の辺は消してから二部マッチングを行えばいいということがいえます。
ではこの命題を証明します。
命題の証明
グラフGの同じ族の頂点同士を結ぶ辺が存在するマッチングを任意にとり固定する。
このとき、辺数を減らさず、同じ族の頂点同士を結ぶ辺の数が真に減るようなマッチングに変形できることをいえばよい。
左右を分ける軸について頂点vと対称な位置にある頂点をv'と書く。すなわちl_i' = r_i, r_i' = l_i (i = 1, 2, …, n)。vとv'を対になった2頂点と呼ぶ。
同じ族にあり、辺で結ばれている2頂点a_0, b_0をとる。
頂点a_0', b_0'に接続する頂点をa_1, b_1とおく。
そのような頂点がどちらか少なくとも一方でも存在しなければそこで止める。
a_1, b_1が対になった2頂点であってもそこで止める。
同じことをインデックスを増やして、止まるまで繰り返す。
各回で新しく得られる頂点a_i, b_iは必ず今までに出てきたことのないものであり、頂点数は有限だからこの繰り返しは必ず止まる。
最後のインデックスをnとしよう。
ここで最後の止まり方には次の3つの場合がある:
(1) a_{n+1}もb_{n+1}も存在しなかった場合
(2) a_{n+1}, b_{n+1}のどちらか片方は存在するが、もう一方は存在しなかった場合
(3) a_{n+1}とb_{n+1}が対になった2頂点だった場合
ほかの場合もほとんど同様なので(1)の場合だけ証明する。
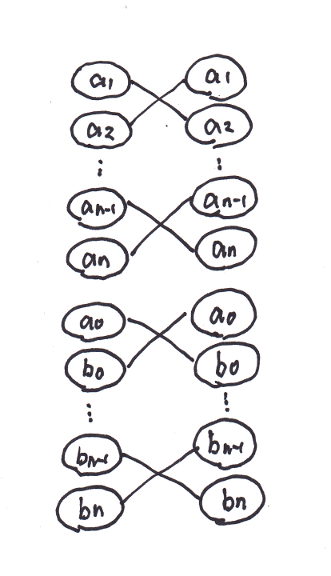
グラフのうち、先の操作で出てきた頂点たちの部分は上の形をしている。
nが奇数なら次のように辺を結び直せばいい。 (対になった2頂点a_0, a_0'などを単に両方ともa_0というラベルで書いている)
nが偶数なら次のように辺を結び直せばいい。
するとどちらの場合も辺の数は2n+1個から2n+2個となり減少はしていない。また同じ族の頂点同士を結ぶ辺は少なくとも1個から0個へ真に減少している。
よって主張は証明された。 □