■
『文章力の基本』(阿部紘久)より。

こういう作文、小中学校のときやってしまっていたなあ。
緯度差1°あたりの経線弧の長さを求めるプログラム
- 高校地学の教科書を読んでいたら計算したくなったので。久しぶりのプログラミング楽しかったです。
- 計算結果は教科書に載っているものと微妙に異なる数値が出てきます。
- 楕円の弧長の近似値を求めるのに区分求積法を使いました。もっと良い方法がありそうです。
- 区分求積法を実装したついでにπの近似値も求めてみたり
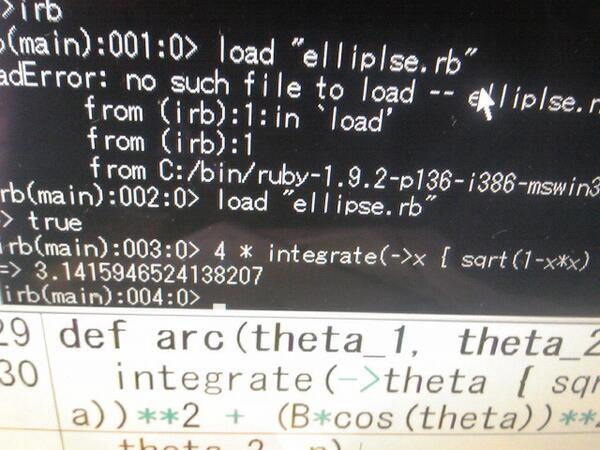
- 調べてみると、緯度差1°あたりの経線弧の長さを求めるという問題からは、どうやら「楕円積分」という話題に発展できるみたいですね。
# 緯度差1°あたりの経線弧の長さを求める include Math A = 6378.137 # 赤道半径 B = 6356.752 # 極半径 N = 50000 # 近似の細かさ EPSILON = 1.0/180*PI # 1° def main p lng(deg2rad(90)) # 極 p lng(deg2rad(66.0 + 20.0/60)) # 北フィンランド p lng(deg2rad(45.0)) # フランス p lng(deg2rad(1.0 + 31.0/60)) # エクアドル p lng(deg2rad(0)) # 赤道 end def deg2rad(deg) deg/180.0*PI end def lng(alpha) theta_1 = alpha_to_theta(alpha-EPSILON/2) theta_2 = alpha_to_theta(alpha+EPSILON/2) arc(theta_1, theta_2, N) end # 楕円の二つの媒介変数の値からその間の弧の長さを求める def arc(theta_1, theta_2, n) integrate(->theta { sqrt((A*sin(theta))**2 + (B*cos(theta))**2) }, theta_1, theta_2, n) end # 緯度αから楕円の媒介変数θの値を得る def alpha_to_theta(alpha) #atan(B/A * tan(alpha)) atan2(B*sin(alpha), A*cos(alpha)) end # 区分求積法により定積分の近似値を計算する def integrate(f, a, b, n) delta_x = (b-a).to_f / n sum = 0.0 n.times do |i| x = a + delta_x * i sum += f.(x) * delta_x end sum end main() if $0 == __FILE__
AtCoder Regular Contest #013 D問題 切り分けできるかな?
AtCoderの過去問としてARC#013をやってみましたが、さんざんな結果でした。
C問題は以下に解説がありますので、ここではD問題の解説をします。
D問題の問題文:
参考にしたソースコード: (蟻本の著者の一人でもあるiwiwiさんによる提出です)
これは二部マッチングに帰着させて解く問題だったようですね。
最大マッチングに帰着できること
最大マッチングに帰着できることは簡単にわかります。
まず必要になる分銅を表す頂点を用意します。つまり作れる分銅の重さがn通りあれば頂点は2n個あります。
次に1つの鉄塊を切断して作ることにする2つの分銅の頂点同士を結びます。このとき必要になる鉄塊の個数は(頂点数) - (辺数)となります。
さて、これを最小化する鉄塊の切断の仕方(すなわち辺の結び方)を作るには、1つの鉄塊を切断して得られる2つの重さであるような異なる2頂点の対をすべて辺で結んでおき最大マッチングを求めればよいのです。
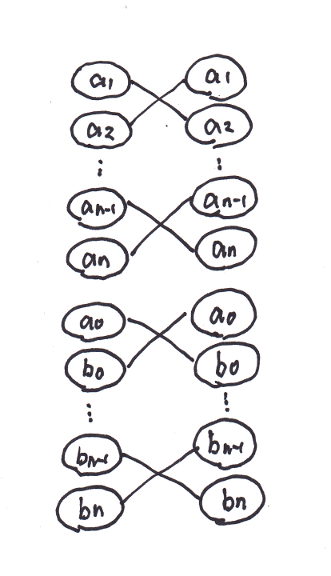
左右対称なグラフの最大マッチングに関する命題
さて二部マッチングに帰着できることは次の命題を証明すればよいです。
G=(V,E)を無向単純グラフとする。
頂点集合Vは同じ要素数の2つの族L = {l_1, …, l_n}, R = {r_1, …, r_n}に分割できるとする。
また、各i, j = 1, 2, …, nについて
l_iとr_jが接続している <=> r_iとl_jが接続している
l_iとl_jが接続している <=> r_iとr_jが接続している
が成り立つとする。このとき同じ族の頂点同士を結ぶ辺を使わない、グラフGの最大マッチングがある。
ラフな言い方をすれば「頂点を左右2つの族に分割できて、グラフが左右対称になるなら、同じ族の頂点同士を結ぶ辺を使わない最大マッチングがある」といったところです。 (最初はもっとこの問題に特殊化した命題を証明したのですが、後日この形に一般化できることを気づきました)
今回の問題のグラフはこの命題の前提を満たします。なぜなら頂点は同じ重さのペアに分けられますが、同じペアの2つの頂点を別々の族に入れればいいからです。
そして、「同じ族の頂点同士を結ぶ辺を使わない最大マッチングがある」ということから、同じ族の頂点同士の辺は消してから二部マッチングを行えばいいということがいえます。
ではこの命題を証明します。
命題の証明
グラフGの同じ族の頂点同士を結ぶ辺が存在するマッチングを任意にとり固定する。
このとき、辺数を減らさず、同じ族の頂点同士を結ぶ辺の数が真に減るようなマッチングに変形できることをいえばよい。
左右を分ける軸について頂点vと対称な位置にある頂点をv'と書く。すなわちl_i' = r_i, r_i' = l_i (i = 1, 2, …, n)。vとv'を対になった2頂点と呼ぶ。
同じ族にあり、辺で結ばれている2頂点a_0, b_0をとる。
頂点a_0', b_0'に接続する頂点をa_1, b_1とおく。
そのような頂点がどちらか少なくとも一方でも存在しなければそこで止める。
a_1, b_1が対になった2頂点であってもそこで止める。
同じことをインデックスを増やして、止まるまで繰り返す。
各回で新しく得られる頂点a_i, b_iは必ず今までに出てきたことのないものであり、頂点数は有限だからこの繰り返しは必ず止まる。
最後のインデックスをnとしよう。
ここで最後の止まり方には次の3つの場合がある:
(1) a_{n+1}もb_{n+1}も存在しなかった場合
(2) a_{n+1}, b_{n+1}のどちらか片方は存在するが、もう一方は存在しなかった場合
(3) a_{n+1}とb_{n+1}が対になった2頂点だった場合
ほかの場合もほとんど同様なので(1)の場合だけ証明する。
グラフのうち、先の操作で出てきた頂点たちの部分は上の形をしている。
nが奇数なら次のように辺を結び直せばいい。 (対になった2頂点a_0, a_0'などを単に両方ともa_0というラベルで書いている)
nが偶数なら次のように辺を結び直せばいい。
するとどちらの場合も辺の数は2n+1個から2n+2個となり減少はしていない。また同じ族の頂点同士を結ぶ辺は少なくとも1個から0個へ真に減少している。
よって主張は証明された。 □
AtCoder Regular Contest #014
AtCoder Regular Contest #014というものに参加しました。プログラミングコンテスト初参加でしたけど楽しめました。
僕が提出した答案はこちら: http://arc014.contest.atcoder.jp/submissions/all?user_screen_name=oupo
A問題とB問題はクリアして、C問題はナイーブな解法で部分点をもらいました。D問題は時間内に解けず、開催時間終了後に提出しました。400点満点で230点です。
4問中2問はプログラミングの基礎知識があれば誰でも解ける問題だったり、UIがシンプルでわかりやすかったりなど初心者への配慮が行き届いているなーという印象を受けました。これなら続けられそうです。あと、問題文にユーモアがあるのがいいですよね。
なお、AtCoderをやってみようという気になったきっかけはこちらの記事です。良い記事ですよ!:
問題C
C: 魂の還る場所 - AtCoder Regular Contest 014 | AtCoder
一次元のぷよぷよ的問題。
各色の個数のmod 2の和が答えになるということですが、解けませんでした><
証明を書いてみる。
ボールを入れていくどの段階においても筒に同じ色のボールは2つ以上ないというような入れ方が存在する
ボールを入れていくどの段階においても筒に同じ色のボールは2つ以上ない、という性質をPとしよう。
Pを満たす入れ方が存在することを与えられるボールの個数に関する帰納法で示す。
与えられるボールの列を一つ固定し、個数をNとする。
このとき、最後の一つのボールを除いたN-1個のボールの列に関する性質Pを満たす入れ方を一つとって固定する (帰納法の仮定により)。
この入れ方をし終わったときの状況を考え、ここへ今考えているN個のボールのうちの最後のボールを入れたい。
入れようとしているボールと同じ色が、この状況の筒になければ、このボールを左右どちらから入れても性質Pを満たす入れ方となり証明は終わる。
入れようとしているボールと同じ色が筒の端にあれば、その側へこのボールを入れれば、性質Pを満たす入れ方になりこの場合も証明は終わる。
それ以外の場合、筒は色の互いに異なる3個のボールからなっていて、真ん中が入れようとしているボールの色である。
仮に今入れようとしているボールの色をG、筒の中の状況をRGBとしよう。
今固定している入れ方において、最後の操作の直前でも、同じ色のボールは2つ以上ないという性質が成立している。よって、最後の操作ではボールは消えていない。
つまり、最後の操作ではRを左から入れたかBを右から入れたかのどちらかである。どちらにしても入れる方向を反対に直せばGが端に来るようになる。ここにGを入れれば、今考えているN個のボール列に関する性質Pを満たす入れ方になる。
□
「与えられたボールの各色の個数のmod 2の和」が答えに、すなわち入れ終わった後の筒の中のボールの数の最小になる
ボールが消えるときには必ず同じ色のボールが2つ消える。よって、どんな入れ方でも結果の筒と与えられたボール列との間で、各色の個数の偶奇は一致する。
上の補題から、結果の各色の個数が1以下になる入れ方が存在する。
ところが偶奇の一致によって、そのような入れ方の結果は次の形に限られる。
筒の中の色Rのボールの数 = (与えられた色Rのボールの個数 mod 2)
筒の中の色Gのボールの数 = (与えられた色Gのボールの個数 mod 2)
筒の中の色Bのボールの数 = (与えられた色Bのボールの個数 mod 2)
このとき、筒の中のボールの数は、「与えられたボールの各色の個数のmod 2の和」となり、偶奇の一致によりこれが最小値であるとわかる。
□
Code Puzzle
任天堂が公開しているCode PuzzleのRuby版をやっています。
今裏問題をクリアしたところです。裏クリアのあとにまだ真クリアが残っているそうですが、まだどうやったらいけるのか見つけれていません。
数独ソルバを書くのが疲れました…。
RGenGCの発表資料を読んだ
ささだこういちさんによるRGenGCの発表資料を読みました。
英語だったので条件反射的にウッとなったのですが印刷してボールペンを片手に辞書を開きながら読み通しました。
RGenGCとは何物か、その仕組みはどうなっているのかということに注目してまとめます。誤りがあれば指摘していただけると助かります。
世代別GCの復習
世代別GCではオブジェクトを新世代と旧世代にわけます。
オブジェクトは最初新世代として生成され、一度でもGCして生き残ったオブジェクトは旧世代となります。ふだんのGC (minor GC)では新世代のみを扱い、旧世代オブジェクトは死んでいても回収しません。たまに行うmajor GCで旧世代も含めてGCします。
- ルートオブジェクトからたどれるオブジェクトにマークをつけます
- マークをつけたオブジェクトは旧世代へ移行します
- ただしマークの最中に旧世代オブジェクトに行き着いた場合、そこから先はtraverseしません
- マーク処理が終わったのち、マークのつかなかった新世代オブジェクトを回収します
さて上の方法だけでは問題があります。マーク時、旧世代オブジェクトからその先はtraverseしないという部分です。これでは旧世代オブジェクトを通してしかルートからたどれない新世代オブジェクトにマークがつきません。
つまり生きているオブジェクトを誤って回収してしまう可能性があります。
そこで旧世代オブジェクトから新世代オブジェクトへの参照関係 (old→new)が発生したら、旧世代オブジェクトの方をRemember Setという集合に入れ、新世代へ移行させます。
そしてRemeber Setをminor GCのマーク時に一つのルートとして扱います。
これで生きているオブジェクトを誤って回収してしまう可能性はなくなりました。
なお、Remember Setに入れたのと同時に新世代へ移行していますが、これをしないとRemember Setからマークしにいこうとしても旧世代だからといってすぐに突っぱねられてしまうからこうしています。
さて、これを実現するためには、オブジェクトに書き込みがあったとき、それがold→newの参照関係を発生させていないかチェックする必要があります。
これをライトバリアといい、オブジェクトの属性に書き込むコードの位置には必ずライトバリアを挿入しなければなりません (Cレベルの話)。
ここがCRubyに世代別GCを導入できない理由でした。ライトバリアを挿入しないといけないとなると、既存の拡張ライブラリとの互換性がなくなり、また開発コストも増大します。
そこでRGenGCです。
RGenGC
RGenGCとはRestricted Generatinal GCの略でライトバリア保護されたオブジェクトとそうでないオブジェクトを同じヒープ内に共存することを許容した新しいGCのアルゴリズムです。RGenGCを導入しても拡張ライブラリの互換性は100%保たれます。
ライトバリア保護されたオブジェクトをsunnyオブジェクト、そうでないオブジェクトをshadyオブジェクトといいます。これをアプリケーション側からみるとshadyオブジェクトは何も気を配らず作ったり書き換えたりできますが、sunnyオブジェクトはきちんと漏らさずにライトバリアを挿入するという注意深さが要求されます。つまりsunnyオブジェクトの方が実装コストは高めです。
もちろんshadyオブジェクトがsunnyオブジェクトよりも少なければ少ないほどGCのパフォーマンスは向上します。
Cレベルのオブジェクト生成時にFL_KEEP_WBというフラグを設定すればsunnyオブジェクトとして生成され、特に指定しなければshadyとなります。sunnyオブジェクトをshady化することは可能ですがその逆はできません。
現在、Array, String, Hash, Object, Numericといったオブジェクトはsunnyオブジェクトとして生成されます。
sunnyオブジェクトをshady化するのは、もう書き換えを追跡しきれない!という状況で使えます。たとえばArrayオブジェクトの実体のポインタを得るRARRAY_PTRというマクロがC APIにありますが、これを使われるともう書き換えは追跡しようがありません。そこでRARRAY_PTRマクロには使われたらshady化するという動作が加えられています。これによってRARRAY_PTRを用いる拡張ライブラリとも互換性を保っています。
結局のところ次の2つの利点がいえます:
- 明示的にsunnyオブジェクトとしてオブジェクトを生成しない限りライトバリア挿入の必要はないので拡張ライブラリの互換性が保たれます
- 一気にすべてのコードをライトバリア対応にすることは困難ですが、徐々にライトバリア対応コードを増やしてGCのパフォーマンスを伸ばしていくことができます
RGenGCの仕組み
RGenGCがどのような仕組みなのか見ていきます。
まずRGenGCの高速化の肝はどこかというと、minor GCのマークフェーズで旧世代オブジェクトより先をたどらないことです。
一方、スイープフェーズは従来通り、ヒープを全て見るのでスピードは変わりません。
さてshadyなオブジェクトとはライトバリアなしで書き換えが行われうるオブジェクトでした。するとshadyなオブジェクトがもし仮に旧世代に移行しても、自身の属性に新世代への参照ができることを検知できません。
したがってshadyなオブジェクトは旧世代に移行せずずっと新世代のままにしておきます。
minor GC
minor GCでのマークフェーズでの処理を考えます。
通常の世代別GCのやり方通りにマークしてマークしたものは旧世代へ、ただしshadyオブジェクトについてはマークしても移行しないという方法はどうでしょうか。
この方法だと旧世代オブジェクトを通さないとルートからたどれない新世代オブジェクトができてしまいます。
そこでこの方法に加えて、shadyオブジェクトをマークするときはもし親が旧世代化したのであればRemember Setへ入れます。これで上の問題は解決します。
なお親という言葉はマーク処理を木構造のtraverseだとして考えたコンテキストで使っています。「親が旧世代化した」以外の場合として「親はなくルートから直接来た場合」、「親がshadyな場合」があります。
shade操作
次にRARRAY_PTRなどによって、オブジェクトがshadyに切り替わる場面を考えます。このshadyに切り替える操作をshade操作といいます。
特に旧世代のsunnyオブジェクトがshadeされる場合が考察を必要とします。
shadyオブジェクトは常に新世代であるとしていたので、このオブジェクトは新世代に移行します。
しかしこのとき、このオブジェクトが「旧世代オブジェクトを通さないとルートからたどれない新世代オブジェクト」と化してしまう可能性があるので、このオブジェクトをRemember Setに入れます。
これがオブジェクトをshadyに切り替えるときに一緒に行うことです。
以上でRGenGCの仕組みを取り上げました。案外あっさりしていますね。